Digitaaltehnika ja digitaalloogika I207
KODUTÖÖ
2017
kaugõpe
 tagasi
tagasi
Selles õppeaines tuleb teha ja vormistatult/köidetult esitada üksainus mitmeosaline kodutöö, mille tähtaeg on jaanuaris.
Kodutöö põhineb ühel konkreetsel osaliselt määratud 4-muutuja loogikafunktsioonil.
1. Leida oma matriklinumbrile vastav 4-muutuja loogikafunktsioon.
Igal õpilasel on oma loogikafunktsioon, mille saamiseks:
— käivitada Windowsi Calculator  ( CALC.EXE ) ja määrata talle seaded View-Programmer ja Dec (kümnendsüsteem) ja Qword:
( CALC.EXE ) ja määrata talle seaded View-Programmer ja Dec (kümnendsüsteem) ja Qword:


— sisestada lahtrisse oma matriklinumber (pildil: 135678 suvalise näitena):
kui matr.numbri koosseisus sisaldub lisaks numbritele ka tähti, siis tähed tuleb ära jätta.
— lülitada kalkulaator ümber 16ndsüsteemile (Hex).

Kalkulaator hakkab näitama eelnevalt sisestatud matriklinumbrit 16ndkujul ( pildil: 211FE).
— kalkulaatoris näidatava 16ndarvu 7-ga korrutamiseks vajutada järjest * ja 7 ning järgnevalt võrdusmärki = korduvalt, kuni näidatav 16ndarv kasvab 7-kohaliseks:
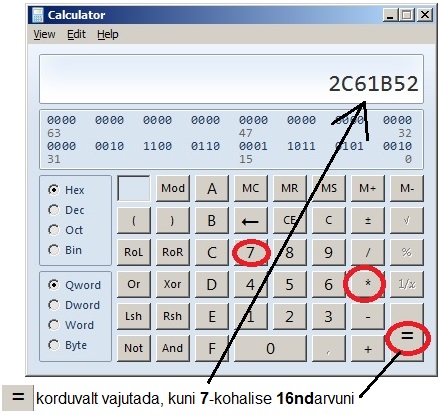
Pildilolevas näites tuleb võrdusmärki vajutada 3 korda, et jõuda 7-järgulise 16ndarvuni 2C61B52
NB! Võrdusmärki vajutades tuleb olla tähelepanelik. Õige on esimene tekkiv 7-kohaline 16ndarv.
Kui =märki vajutada hooletult 1....2 korda vajalikust rohkem, siis võib ka üleliia korrutatud 16ndarv olla endiselt 7-kohaline — kuid ta on genereeritava funktsiooni jaoks juba vale!
Saadud 16ndarv võib sisaldada numbrimärke 0 1 2 3 4 5 6 7 8 9 A B C D E F kus 16ndnumbrid A B C D E F omavad väärtusi:
A = 10
B = 11
C = 12
D = 13
E = 14
F = 15
Saadud 16ndarvu 7 järguväärtust 0 . . . 15 määravad loogikafunktsiooni 1-de piirkonna. Korduvaid järguväärtusi ehk numbrimärkide topeltesinemisi (siin näites: number 2) tuleb ignoreerida.
Pildilolevas näites olev korrutamistulemus (7-kohaline 16ndarv 2C61B52) määrab 4-muutuja loogikafunktsiooni 1de piirkonna (numbrilises 10ndesituses):
1 2 5 6 11 12
(kuna numbreid 2 on selles 16ndarvus mitu, siis arvestame teda ühekordselt)
Määramatuspiirkonna leidmine:
— eelkirjeldatud viisil toimides saadud ja hetkel kalkulaatoris näidatava 16ndarvu (siin näites: 2C61B52) tuleb korrutada 7-ga veel niimitu korda, kuni arv kasvab 9-järguliseks — ehk tuleb vajutada järjest =-märki veel paar korda, kuni 16ndarv kasvab 9-kohaliseks:
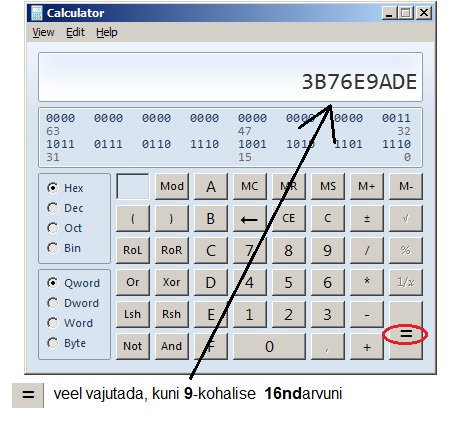
Võtta tuleb korrutamisel esimesena tekkiv 9-kohaline 16ndarv!
9-kohalise tekkinud 16ndarvu (siin näites: 3B76E9ADE ) need järguväärtused 0 . . . 15, mis ei kuulu juba 1-de piirkonda, moodustavad funktsiooni määramatuspiirkonna.
Pildilolevas näites on määramatuspiirkond seega: 3 7 9 10 13 14 kuna 6 ja 11 (B) kuuluvad juba 1-de piirkonda.
Korduvaid numbreid arvu koosseisus (siin: E ehk 14) arvestame jällegi ühekordselt.
Ülejäänud arvud vahemikus 0....15 (mis puuduvad nii 1de piirkonnas kui ka määramatuspiirkonnas) moodustavad 0de piirkonna.
Siin näites jäävad 0de piirkonna arvudeks: 0 4 8 15 (ehk F)
Seega oleks matriklinumbrile 135678 vastav 4-muutuja loogikafunktsioon oma numbrilises 10ndesituses:
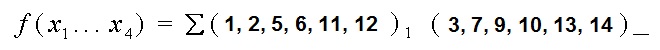
Veelkord täpsustuseks: Te ei pea võtma mitte SEDASAMA ülalnäidatud funktsiooni, vaid tuleb arvutada oma matriklinumbrist alustades ja ülaltoodud toimingud läbides OMA loogikafunktsioon.
Eelnev näidisfunktsioon oleks õige ainult matriklinumbri 135678 omanikule.
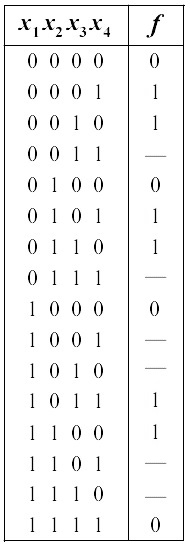
Näitefunktsiooni tõeväärtustabel on:
Lahendatavad ülesanded
2. (kaal: 3%) Kirjutada välja oma matriklinumbrist leitud osaliselt määratud 4-muutuja loogikafunktsiooni tõeväärtustabel.
3. (kaal: 21%) Leida Karnaugh' kaardiga MDNK (minimaalne DNK) ja MKNK (minimaalne KNK), mis sobiksid matriklinumbrist leitud osaliselt määratud 4-muutuja funktsiooni esitamiseks.
(Leitud MDNK ja MKNK ei pea olema teineteisega võrdsed ehk määramatuspiirkonna võib MDNK ja MKNK jaoks "lõpuni määrata" erinevalt.)
Mitme erineva võrdse keerukusega MDNK leidumisel võib nendest vabalt valida ühe suvalise MDNK.
Mitme erineva võrdse keerukusega MKNK leidumisel võib nendest vabalt valida ühe suvalise MKNK.
4. (kaal: 5%) Kirjutada oma funktsiooni 1-de piirkonnast välja täielik DNK (TDNK) (ignoreerides määramatuspiirkonda).
5. (kaal: 12%) Lihtsustada loogikaalgebra põhiseoste abil eelnevalt leitud täielikku DNK-d lihtsaima DNK-ni, milleks see TDNK lihtsustub.
Võrrelda lihtsustamisel saadud DNK-d eelnevalt (punktis 3) leitud MDNK-ga:
— kas nad on võrdsed?
— kui nad pole võrdsed, siis kumb nendest on väiksema keerukusega (ehk lihtsam) avaldis ja miks?
Kõik järgnevad tegevused toimuvad (punktis 3) leitud MDNK-ga ja MKNK-ga. Algne osaliselt määratud funktsioon enam vajalik pole.
6. (kaal: 5%) Leida ja näidata, milleks (0 või 1) väärtustuvad (punktis 3) leitud MDNK ja MKNK määramatuspiirkonna kõikide argumentvektorite korral.
Otsustada (hinnata), kas leitud MDNK ja MKNK on teineteisega võrdsed või mitte.
7. (kaal: 9%) Realiseerida (punktis 3) MDNK-na saadud loogikafunktsioon minimaalseima keerukusega loogikaskeemina, kasutades vabaltvalitud loogikaelemente AND OR ja NOT.
Avaldise keerukuse vähendamiseks võib MDNK-d võimaluse korral teisendada mittenormaalkujuliseks lihtsamaks loogikaavaldiseks.
Loogikaelementide sisendite arv skeemis pole piiratud ja see võib erinevatel elementidel olla erinev. Taotleda, et loogikaelementide summaarne sisendite arv koostatud skeemis oleks vähim.
8. (kaal: 8%) Realiseerida (punktis 3) MKNK-na saadud loogikafunktsioon minimaalseima keerukusega loogikaskeemina elementidel AND OR NOT.
Loogikaelementide sisendite arv skeemis pole piiratud ja see võib erinevatel elementidel olla erinev. Taotleda, et loogikaelementide summaarne sisendite arv koostatud skeemis oleks vähim.
9. (kaal: 12%) Realiseerida (punktis 3) MDNK-na saadud loogikafunktsioon lihtsaima loogikaskeemina kahe sisendiga loogikaelementidel (OR-NOT) .
Näidata ära ka skeemi koostamisele eelnev MDNK üleviimine kujule VÕI-EI ja sisendite piiratud arvu (2) arvestamine.
10. (kaal: 10%) Realiseerida (punktis 3) MKNK-na saadud loogikafunktsioon lihtsaima loogikaskeemina kahe sisendiga loogikaelementidel (AND-NOT) .
Näidata ära ka skeemi koostamisele eelnev MKNK üleviimine kujule JA-EI ja sisendite piiratud arvu (2) arvestamine.
11. (kaal: 15%) Modelleerida punktides 4, 7, 8, 9, 10 saadud tulemusi VHDL-is.
Esitada nii VHDL-kood kui ka simulatsiooni tulemused (lainekujud).
Kasutada võib suvalist simulaatorit.
Soovitav on sisendsignaalid X1....X4 genereerida selliselt, et kaetud on ainult 1-de ja 0-de piirkonnad.
Funktsioonide kirjeldamisel võib kasutada suvalist stiili.
Järgneva näitena on esitatud ühele konkreetsele matr.numbrile vastava funktsiooni modelleerimistulemused punktides 4, 9, 10 ning
VHDL-kood.
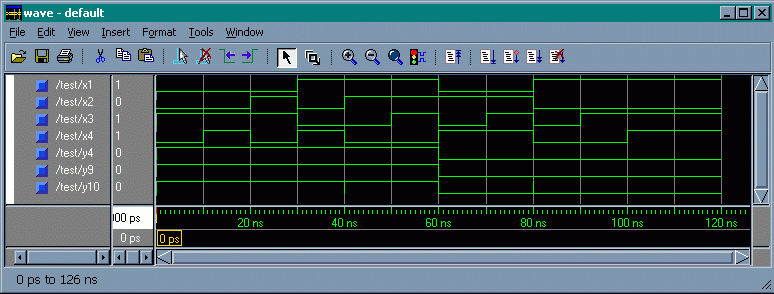
VHDL näide
Vormistus
Kodutöö on soovitav esitada köidetult paberil.
Töö peab olema A4 formaadis ja peab algama tiitellehega:

Kui töö esitatakse käsikirjas, siis peab ta olema mahatõmbamisteta ja parandusteta. Eelistatud on arvutil vormistatud ja väljatrükitud kodutöö.
Lahtisi kokkuköitmata (klambritega kinnitamata) paberilehti mitte esitada.
Parim on lehed kokkukinnitada klambrilööjaga, üheainsa klambriga lehe vasakul ülaservas.
"Tavalised" kirjaklambrid ei sobi:

Hindamine
Kodutöö hinnatakse kuni 100 punktini. Kodutöö tulemus osaleb koos eksamitulemusega aine lõpphinde määramisel.
Kodutöö võib olla määratud kaitsmisele. Kaitsmisele määratud kodutöö saab hinde pärast kaitsmist.
Tähtaeg
Kaugõppe kodutööde tähtaeg on esmasp. 8. jaanuar. (eksamiaeg selgub detsembris)
Pärast semestri õppetöö lõppu saab kodutööd esitada ka ICT maja (Akadeemia tee 15a) postkasti ARVUTITEHNIKA INSTITUUT
Võimalik on saata ka postiga (A4 ümbrikus) aadressile ARVUTITEHNIKA INSTITUUT Akadeemia tee 15a Tallinn 12618
Failina saab esitada (saata e-mailiga) kodutööd eelkõige erandjuhtudel — kui paberil teda enam esitada ega postiga saata ei õnnestu.
Failina esitatav kodutöö tuleb saata e-mailiga AINULT aadressile:
lrv@itcollege.ee
Sobivaimad failiformaadid:
.PDF
PostScript (.ps .prn)
Muud võimalikud (mittesoovitavad) formaadid, kus taasesituse autentsus pole tagatud:
HTML nii failina kui ka lingina (URL-ina)
Rich Text Format (.RTF)
MS Word Document (.DOC)
OpenOffice Document (.SXW)
StarOffice Document (.SDW)
JÕUDU TÖÖLE !
 tagasi
tagasi
 hl@cc.ttu.ee
hl@cc.ttu.ee
 hl@cc.ttu.ee
hl@cc.ttu.ee
 tagasi
tagasi  ( CALC.EXE ) ja määrata talle seaded View-Programmer ja Dec (kümnendsüsteem) ja Qword:
( CALC.EXE ) ja määrata talle seaded View-Programmer ja Dec (kümnendsüsteem) ja Qword:




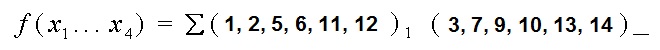




 tagasi
tagasi